5 Osnove linearnih modela

5.1 Regresija

Cilj regresije je da nadje funkcionalnu vezu izmedju obeležja \(Y\), koje nazivamo zavisnom promenljivom i obeležja \(X\), koje nazivamo nezavisnom promenljivom ili prediktorom.

Ova veza je oblika \[Y = f(X) + \varepsilon,\] gde je \(\varepsilon\) slučajna greška modela, koja je nezavisna od \(X\).

Prava funkcija \(f(x)\) je nepoznata, pa je treba oceniti na osnovu uzorka \((x_i, y_i),\ i=1,\dots,n\). Za uzorak pretpostavljamo da važi \[y_i = f(x_i) + \varepsilon_i,\] gde za \(\varepsilon_i\) pretpostavljamo da su nezavisni i \(\varepsilon_i\sim\mathcal{N}(0,1)\), a potrebna nam je ocena \(\hat{f}(x)\).

Prostor svih mogućih funkcija \(f(x)\) je prevelik i nije ga moguće istražiti u potpunosti, pa stoga uvek pretpostavljamo odredjen (obično parametarski) oblik funkcije \(f(x)\), čime smanjujemo prostor funkcija nad kojim tražimo \(f(x)\).

5.2 Linearna regresija

U linearnoj regresiji, pretpostavljamo da je funkcija koju tražimo oblika \(f(x)=\beta_0+\beta_1x,\) odnosno imamo model \[y_i=\beta_0+\beta_1x_i+\varepsilon_i.\] Sada nam se zadatak nalaženja funkcije \(f(x)\) sveo na odredjivanje parametara \(\beta_0\) i \(beta_1\) koji najbolje opisuju podatke.

To se može raditi na mnogo načina, što pokazuje sledeći primer, koji koristi različite metode za ocenu.

5.2.1 Šta znači najbolje?

Koristićemo podatke cars (ugradjene u R) koji prikazuju brzinu vozila i dužina puta potrebnog da se zaustavi. Podaci su za automobile iz 20-ih godina 20. veka. Za ocenu najbolje prave, koristićemo funkcije lm (ugradjena u R) i funkciju rq iz paketa quantreg.

# install.packages("quantreg")
library(ggplot2)
library(quantreg)

## Loading required package: SparseM

## 
## Attaching package: 'SparseM'

## The following object is masked from 'package:base':
## 
##     backsolve

ggplot(cars, aes(x=speed, y=dist)) +
geom_point() +
geom_smooth(method="lm", se = FALSE, color="blue") +
geom_smooth(method="rq", se = FALSE, color="red")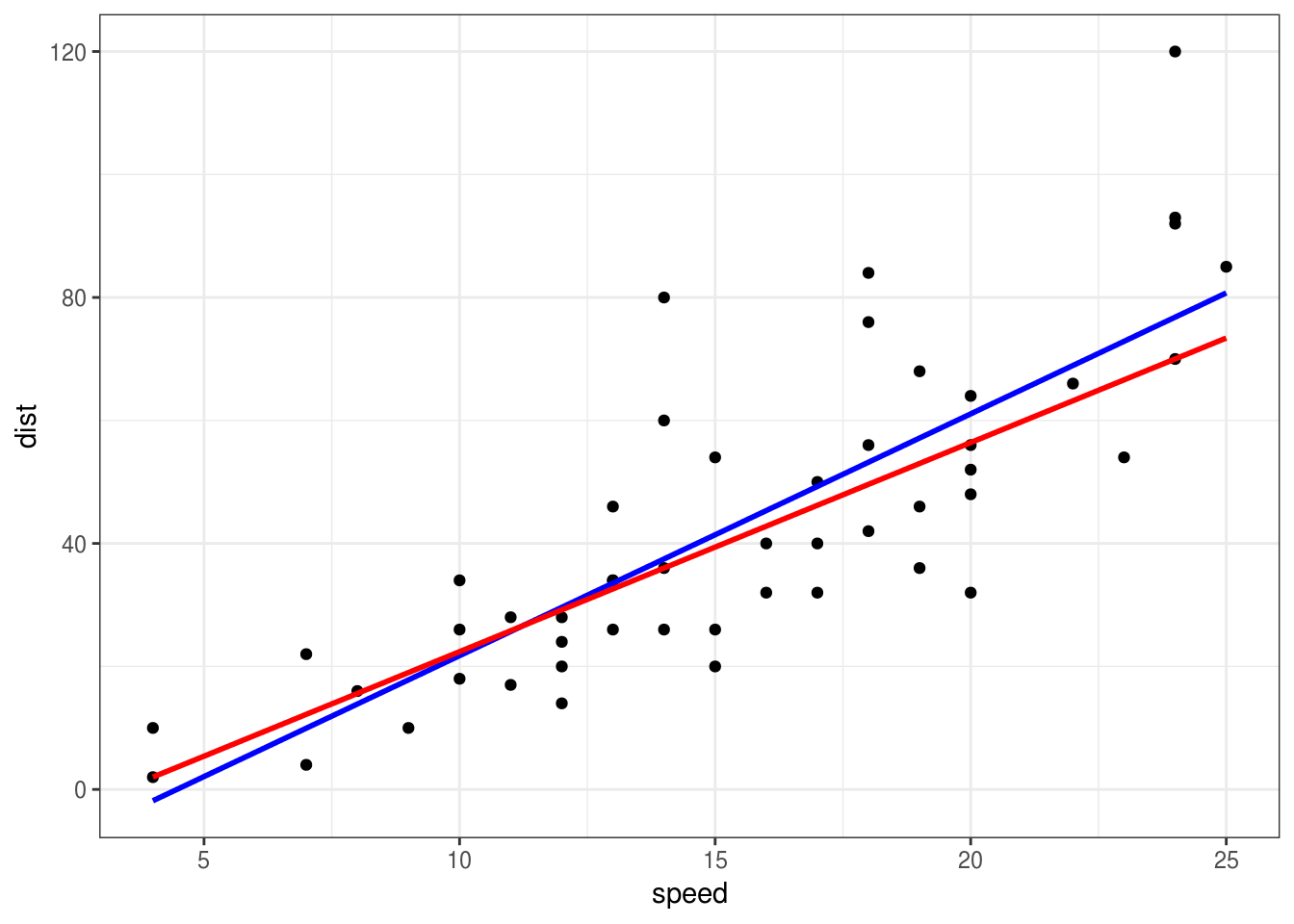

Koja od ove dve prave bolje modeluje podatke?

Ovo pitanje je pogrešno. Treba definisati koji je kriterijum da je nešto bolje od nečeg drugog.

Obe ove prave su dobijene tako da budu optimalne u nekom smislu. Plava je dobijena da bude optimalna u srednjekvadratnom smislu, dok je crvena dobijena kao optimalna u srednjeapsolutnom smislu. Oba metoda su dobra, koji ćemo da koristimo zavisi od prirode podataka koje imamo i cilja istraživanja.

U nastavku ćemo rekreirati ove prave samostalno.

5.2.2 Nalaženje optimalne prave

Najčešći pristup traženju optimalnih vrednosti parametara \(\beta_0\) i \(\beta_1\) je metod najmanjih kvadrata, čiji je cilj minimizovanje srednjekvadratne greške \[\frac1n \sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)^2,\] tj. minimizujemo srednjekvadratno odstupanje stvarnih vrednosti \(y_i\) i ocenjenih vrednosti \(\hat{y}_i=\hat{\beta}_0+\hat\beta_1x_i\).

Dakle, ocenjeni parametri su \[(\hat{\beta}_0,\hat\beta_1) = \underset{\beta_0,\beta_1}{\mathrm{argmin}}\frac1n \sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)^2.\]

Ove parametre nalazi funkcija lm.

U slučaju funkcije rq, parametri su \((\hat{\beta}_0,\hat\beta_1) = \underset{\beta_0,\beta_1}{\mathrm{argmin}}\frac1n \sum_{i=1}^n|y_i-\beta_0-\beta_1x_i|.\)

Primenimo sada stečeno znanje optimizacije da nadjemo tražene ocene

mse <- function(beta) {
  with(cars, {
    mean((dist - beta[1] - beta[2]*speed)^2)
  })
}

beta_hat <- nlm(mse, c(0,0))$estimate


ggplot(cars, aes(x=speed, y=dist)) +
geom_point() +
geom_smooth(method="lm", se = FALSE, color="blue") +
geom_abline(intercept = beta_hat[1], slope = beta_hat[2])

Vidimo da smo pogodili pravu. Uradite isto i za apsolutnu grešku i funkciju rq.

5.2.3 Višestruka linearna regresija

Korišćenje samo jednog prediktora je često nedovoljno, pa se može uvesti i više prediktora u model, koji postaje \[Y = \beta_0+\beta_1X_1+\dots+\beta_pX_p+\varepsilon,\] a kada pravu treba oceniti na osnovu uzorka \((x_{1i},x_{2i},\dots,x_{pi}, y_i),\ i=1,\dots,n\), za uzorak pretpostavljamo da važi \[y_i = \beta_0+\beta_1x_{1i}+\dots+\beta_px_{pi} + \varepsilon_i,\] gde za \(\varepsilon_i\) pretpostavljamo da su nezavisni i \(\varepsilon_i\sim\mathcal{N}(0,1)\).

Optimalne koeficijente ocenjujemo na isti način kao pre, samo imamo više koeficijenata:

\[(\hat{\beta}_0,\hat\beta_1,\dots,\hat\beta_p) = \underset{\beta_0,\beta_1,\dots,\beta_p}{\mathrm{argmin}}\frac1n \sum_{i=1}^n(y_i-\hat\beta_0 - \hat\beta_1x_{1i} -\ldots- \hat\beta_px_{pi})^2.\]

5.3 Linearni modeli u R-u

Glavna funkcija za pravljenje i analiziranje linearnih modela u R-u je funkcija lm. Ona prima kao prvi argument formulu u obliku y ~ x1 + x2 + x3, gde je sa leve strane ~, ovde y, zavisna promenljiva, a sa desne prediktori, gde znak + označava da se prediktor treba uključiti.

Specijalna oznaka za prediktore je . (npr. y ~ .) koja označava da se za prediktore uzmu sve kolone iz tabele, izuzimajući zavisnu promenljivu. Dakle, u suštini . znači “sve ostale promenljive iz podataka”. Uz . se često koristi i - koji označava koje prediktore zanemariti. Na primer, ako imamo kolone x1, x2, x3, y, formula y ~ . - x2 je ekvivalentna y ~ x1 + x3, i znači da treba modelovati y preko x1 i x3.

Drugi argument funkciji lm je data.frame koji sadrži podatke.

Model koji smo posmatrali za skup podataka cars se dobija kao:

model <- lm(dist ~ speed, cars)
model

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Coefficients:
## (Intercept)        speed  
##     -17.579        3.932

Kada pozovemo geom_smooth(method = "lm"), ggplot u poozadini napravi model lm(y~x, data) i njega nacrta.

Najčešće korišćena funkcija uz lm (koja pravi model), je funkcija summary koja prikazuje osnovne rezultate modelovanja

summary(model)

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.069  -9.525  -2.272   9.215  43.201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
## speed         3.9324     0.4155   9.464 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared:  0.6511, Adjusted R-squared:  0.6438 
## F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

Najviše pažnje ćemo posvetiti tabeli sa naslovom “Coefficients”. Ona sadrži 4 kolone, gde se svaki red odnosi na odgovarajući prediktor (u ovom slučaju imamo slobodan član – \(\beta_0\) i koeficijent uz prediktor speed – \(\beta_1\)). Kolone su sledeće:

Estimate: Ocenjena vrednost koeficijenta uz prediktor
Std. Error: Standardna greška ocene koeficijenta (\(se(\hat\beta_j)\))
t value: Vrednost t statistike, koja se koristi za testiranje značajnosti koeficijenata
Pr(>|t|): p vrednost t testa značajnosti odgovarajućeg koeficijenta
zvezdice pored p vrednosti označavaju sa kojim nivoom značajnosti bi dobili statistički značajan rezultat (3 zvezdice predstavljaju p vrednost koja je manja od 1 promila).

Testiranje značajnosti koeficijenata

U tabeli koeficijenata dobijamo neke rezultate testiranja značajnosti koeficijenata. Pri tom testiranju testiramo da li je koeficijent \(\beta_j\) statistički značajan, odnosno, da li se može izbaciji iz modela, a da to ne utiče na kvalitet. Formalno, testiramo \[H_0: \beta_j=0\quad H_1:\beta_j\neq0,\] dok je test statistika koja se koristi \[t = \frac{\hat\beta_j}{se(\hat\beta_j)} \sim t_{n-p-1},\] gde je \(p\) broj prediktora (u slučaju proste regresije, sa 1 prediktorom, \(p=1\)).

5.3.1 Koeficijent determinacije

Za proveru kvaliteta našeg modela, možemo koristiti koeficijent determinacije \[R^2 = 1-\frac{\sum_{i=1}^n(y_i - \hat y_i)^2}{\sum_{i=1}^n(y_i-\bar{y})^2},\] gde je \(\hat y_i = \hat\beta_0 + \hat\beta_1x_{1i} +\ldots+ \hat\beta_px_{pi}\), a \(\bar y=\frac1n\sum_{i=1}^ny_i\). Što je veči koeficijent determinacije, to je model bolji. Najveća moguća vrednost je 1.

Intuitivno, vidimo da poredimo srednjekvadratnu grešku našeg modela (\(\hat y\)) i srednjekvadratnu grešku konstantnog modela koji \(y\) uvek ocenjuje sa prosekom \(\bar y\). Očekivano je, ako je naš model dobar i ako postoji zavisnost izmedju prediktora i zavisne promenljive, da će prava (hiperravan) koju mi dobijemo bolje opisivati podatke od horizontalne linije (hiperravni) odredjene prosekom.

Koeficijent determinacije \(R^2\) je ime dobio, jer zaista jeste kvadrat korelacije \(y\) i \(\hat y\).

summary(model)

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.069  -9.525  -2.272   9.215  43.201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
## speed         3.9324     0.4155   9.464 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared:  0.6511, Adjusted R-squared:  0.6438 
## F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

cor(cars$dist, fitted(model))^2

## [1] 0.6510794

Vidimo da su Multiple R-squared iz sažetka modela i kvadrat korelacije oba jednaka 0.65.